The GigaTroller is the motor controller designed for running the absorber on the motor dyno, named for the absurd mosfets it uses, the IXYS MMIX1F520N075T2 TrenchT2 GigaMOS HiperFET. What a mouthful.
This is an rediculous mosfet. Rdson is quite good but not spectacular (given its size), typically 1.2 mΩ on a 75V FET, and it has quite a lot of gate charge, 550 nC at 10V on the gate. However, mechanically it's pretty awesome. It's some fancy IXYS surface mount package, 1" square, with an isolated metal pad on the top. Thanks to the presumably gigantic die and excellent package, it's rated for 500 A at 25 C, 1700 A pulsed, and 830 (!) watts of package dissipation at 25 C. It's also a whopping $17 per FET on Digikey, but fortunately Bayley found some rails of them for $5 each on Ebay. At $17 they would be silly to buy but it's actually a pretty reasonable amount of transistor for $5.
Nominally I'm designing this controller for 200A, 50V operation, because that's all the dyno absorber can do. This should be very safely within the ratings of these transistors.
A tricky thing about designing a high current controller like this is designing a PCB that can actually handle that current. To make the controller as compact as possible, I designed it to use custom surface-mount busbar, which I waterjet cut out of copper plate and reflowed to the PCB. Another interesting feature of this transistor package is that it physically has a cutaway underneath the package between the legs. I'm using that space to route the busbar beneath the transistors, instead of next to them.
Here's a board from 3PCB and a pile of busbar. Although I didn't ask for gold plating on the PCB, I got it for no extra cost. Presumably my boards were tacked onto a big batch that was getting plated or something?
It took two tries to solder the bus bar. First time around, I tried clamping everything at once and baking it in an oven, but that ended up warping the board and turning out poorly. At Peter's suggestion, I soldered the busbars one-at-a-time, fixturing them with steel binder clips and heat-gunning them with solder paste underneath. This worked out beautifully:
After sanding off excess solder and oxidation:
Here's the power board populated with FETs, Allegro current sensors, gate pulldowns and gate zeners, and one 22 uF film cap per leg. After reading this paper, I decided to try out using just a small-ish set of film caps instead of the the huge pile of electrolytics I'm used to seeing.
Note the bus bar routed underneath the transistors:
Logic and gate drive stack on top of the controller, next to the capacitors. An STM32F446 does all the motor-control stuff. I know the F3 series are probably a better choice for motor control things, but I had a few F446's left lying around, and this way I could just port all my FOC code over from my small controllers with minimal editing.
The power supply section of this features 5 isolated 15V DC supplies - one for the low-side gate drivers, one for each of the three high-side gate drivers, and one one for the logic. The gates are driven by 2.5A gate drive optoisolators.
Bayley actually designed the power supply and gate drive section of this for different motor control project of similar power level, so I borrowed his design. A 555 generates a square wave, which is fed into the inputs of a dual inverting/non-inverting gate drive IC. The gate driver swings around the primary of a 6-winding transformer, the 5 other windings of which are rectified to generate the 5 isolated 15V supplies.
The gate drive IC driving the transformer gets extremely warm, but its power dissipation is still within spec, and it's now operated 10's of hours at least with no problems. When the controller gets mounted to a heatsink I'll make sure it gets some airflow too.
I used ethernet connectors for programming/serial and position sensor, because they're nice cheap, locking, small-footprint connectors. And they're matte black.
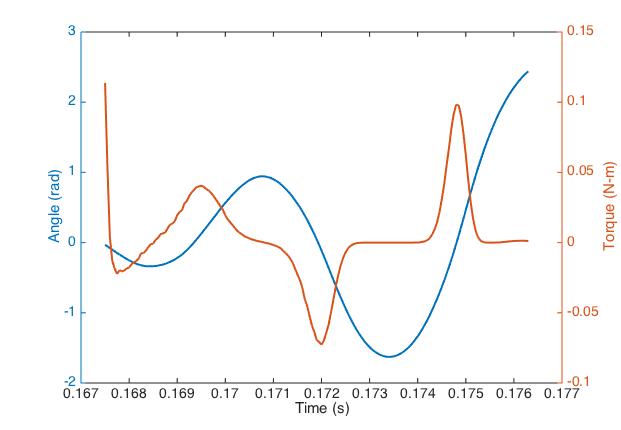
To get the controller working, I spent a few days figuring out how to generate complimentary PWM signals with software-defined deadtime. That was the only significant code change, though, other than re-doing the current loops as usual.
So far I've pushed the controller to 45V, 100 phase-amps entirely without drama. The transistors get a little warm. Here's what bus voltage looks like at ~80 phase amps. Note this is running of a bench supply with several feet of wire between the supply and controller. At 41 volts on the supply, the sharp spikes hit ~7.5 volts above nominal, and the bulk ripple is a couple volts.
Here are the Eagle files, if for some reason you want to build one of these:
Power Board
Logic Board